
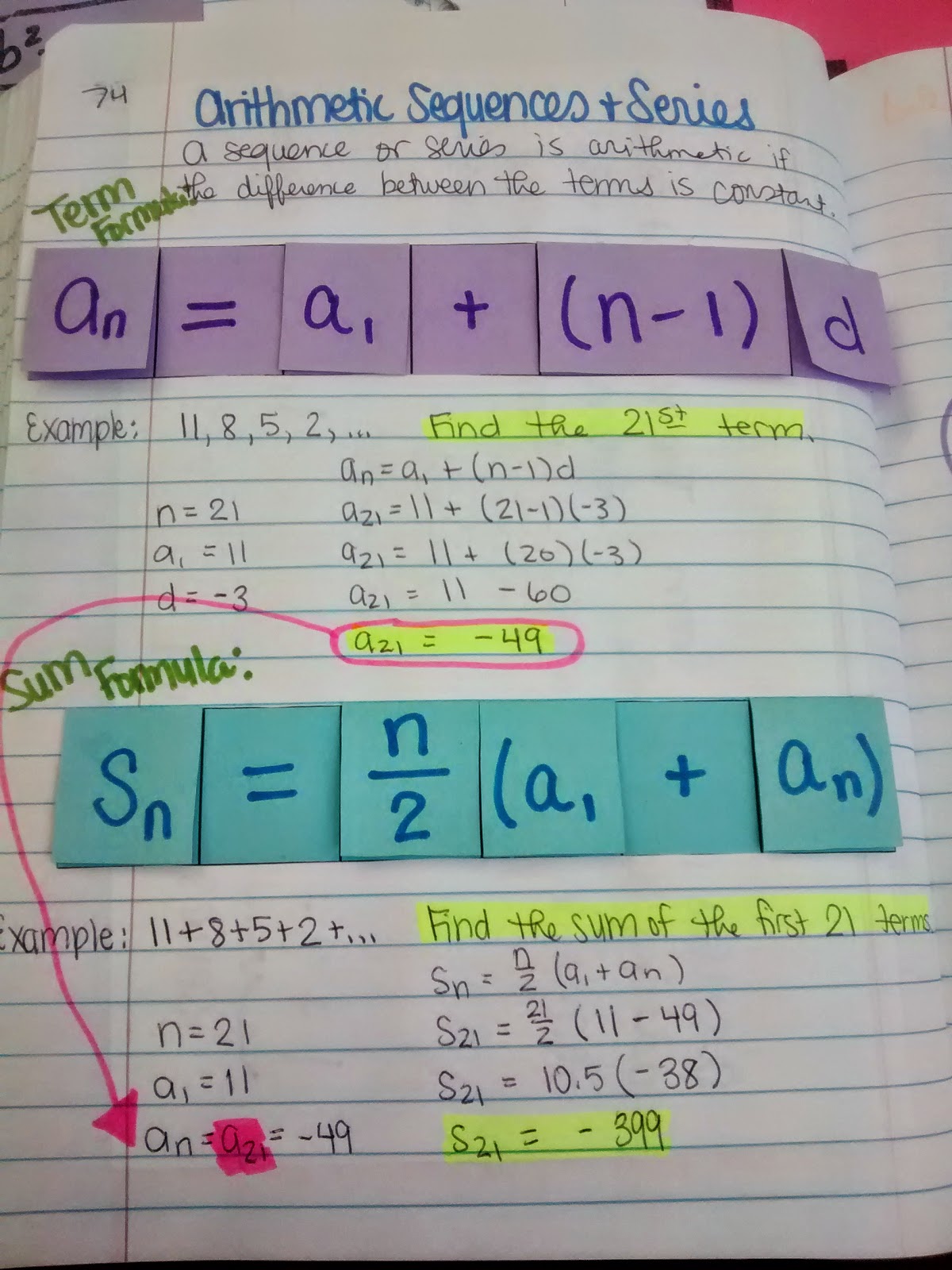
Infinite sequences, on the other hand, contain an unlimited number of values for k. Because there are four values of k, the sequence only contains 4 numbers and is therefore finite. For example, the first finite sequence that Sal lists has values of k from 1 to 4. The value of the \(n^ = d\), for all successive In a finite sequence, there are a limited number of values for k. \) with the specific property that the difference between two consecutive terms of the sequence is ALWAYS constant, equal to a certain value \(d\). Learn more about this arithmetic sequences calculator so you can better interpret the results provided by this solver: An arithmetic sequence is a Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License. Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, Then you must include on every physical page the following attribution: If the rule is to add or subtract a number each time, it is called an arithmetic sequence. If you are redistributing all or part of this book in a print format, Sequences Number sequences are sets of numbers that follow a pattern or a rule. Want to cite, share, or modify this book? This book uses the Round to the nearest thousandth when necessary. Use the right arrow key to scroll through the list of terms.įor the following exercises, use the steps above to find the indicated terms for the sequence. Press to see the list of terms for the finite sequence defined.See the instructions above for the description of each item. Enter the items in the order “Expr”, “Variable”, “start”, “end” separated by commas.Plug your numbers into the formula where x is the slope and youll get the same result: 5 + x (10 1) 59. Use the right arrow key to scroll through the list of terms. Your shortcut is derived from the explicit formula for the arithmetic sequence like 5 + 2 (n 1) a (n). Press to see the list of terms for the finite sequence defined. You will see the sequence syntax on the screen. Press 3 times to return to the home screen.In the line headed “end:” key in the value of n n that ends the sequence.In the line headed “start:” key in the value of n n that begins the sequence.In the line headed “Variable:” type in the variable used on the previous step.In the line headed “Expr:” type in the explicit formula, using the button for n n.Scroll over to OPS and choose “seq(” from the dropdown list.For example, suppose we know the following:įind the tenth term of the sequence a 1 = 2 a 1 = 2, a n = n a n − 1 a n = n a n − 1įollow these steps to evaluate a finite sequence defined by an explicit formula. Instead, we describe the sequence using a recursive formula, a formula that defines the terms of a sequence using previous terms.Ī recursive formula always has two parts: the value of an initial term (or terms), and an equation defining a n a n in terms of preceding terms. The Fibonacci sequence cannot easily be written using an explicit formula. Other examples from the natural world that exhibit the Fibonacci sequence are the Calla Lily, which has just one petal, the Black-Eyed Susan with 13 petals, and different varieties of daisies that may have 21 or 34 petals.Įach term of the Fibonacci sequence depends on the terms that come before it. It provides plenty of examples of finding patterns in arithmetic and.
SEQUENCES ALGEBRA HOW TO
Their growth follows the Fibonacci sequence, a famous sequence in which each term can be found by adding the preceding two terms. This pre-algebra video tutorial explains how to find the next term in a number series. We may see the sequence in the leaf or branch arrangement, the number of petals of a flower, or the pattern of the chambers in a nautilus shell.


Sequences occur naturally in the growth patterns of nautilus shells, pinecones, tree branches, and many other natural structures. Writing the Terms of a Sequence Defined by a Recursive Formula


 0 kommentar(er)
0 kommentar(er)
